개인적으로 가장 어려워하면서도, 가장 흥미가 있는 주제인 LCA 문제이다.
사실 처음부터 lca 문제를 해결하려던 건 아니고, 트리 문제를 구경하던 중 lca가 떠오르는 문제를 발견하여 lca 연습 겸 풀어본 문제이다.
https://www.acmicpc.net/problem/13511
13511번: 트리와 쿼리 2
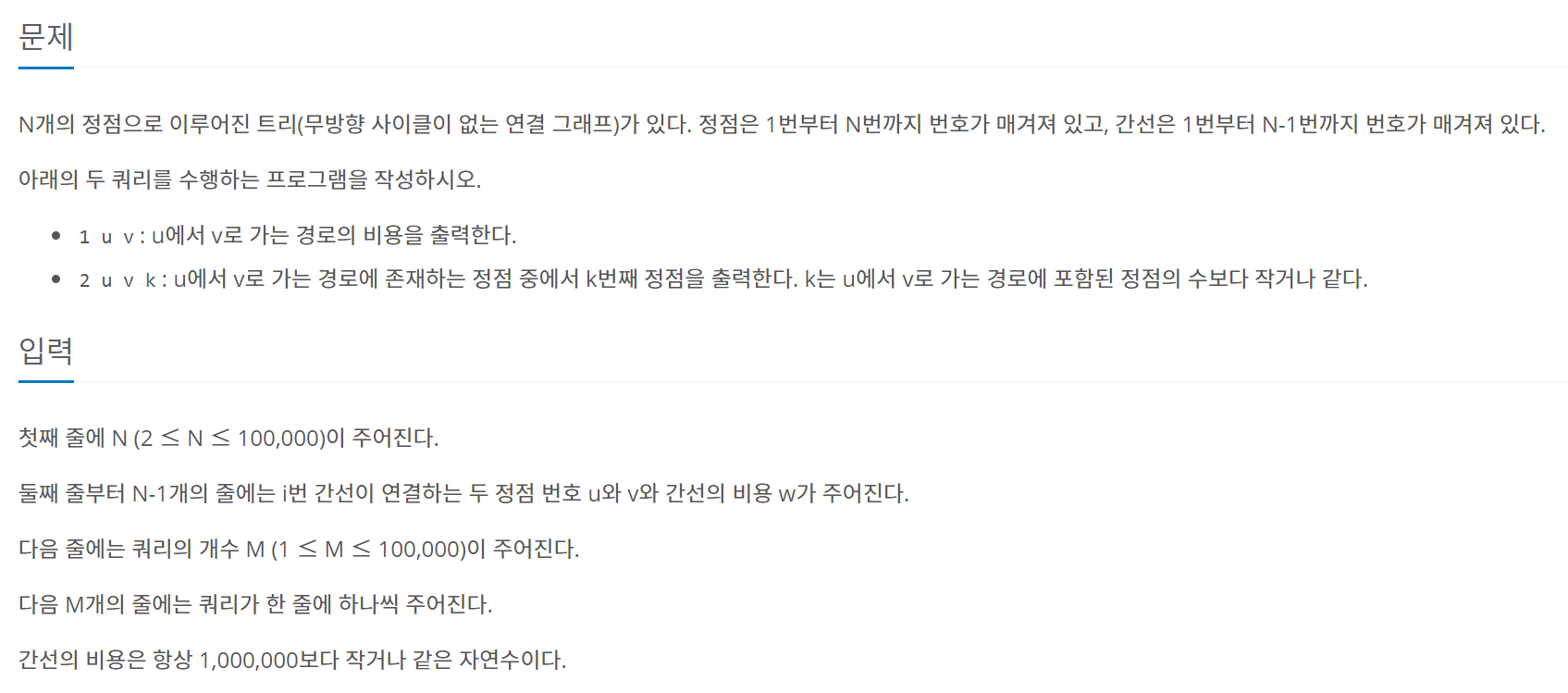
N개의 정점으로 이루어진 트리(무방향 사이클이 없는 연결 그래프)가 있다. 정점은 1번부터 N번까지 번호가 매겨져 있고, 간선은 1번부터 N-1번까지 번호가 매겨져 있다. 아래의 두 쿼리를 수행하
www.acmicpc.net
- 상한 시간복잡도: O(NlgN)
- 사용 알고리즘: LCA
LCA 코드 살펴보기
LCA를 O(lgN)의 속도로 찾아내야 상한 시간복잡도를 넘기지 않는다.
루트노드의 번호가 정해져있지 않지만, 이미 트리의 형태는 정해져있기 때문에 우리가 임의로 1번 노드를 루트로 지정해도 상관이 없다.
void init(int cur) {
for (auto i : v[cur]) {
// 자식노드의 트리의 높이가 지정이 돼있지 않다면
if (d[i.second] == -1) {
// 자식노드의 높이는 부모노드보다 1 큼
d[i.second] = d[cur] + 1;
// 루트에서부터 현재 노드까지의 거리
len[i.second] = len[cur] + i.first;
// 2^0번째 부모 노드는 cur
p[i.second][0] = cur;
// 재귀적으로 2^k번째 자식 노드의 높이, 거리, 부모정보 설정
init(i.second);
}
}
}위 코드로 노드들의 2^0번째, 즉 첫번째 부모노드의 정보를 설정할 수 있다.
for (int j = 0; j < SIZE; j++) {
// i=1일 때는 루트노드. 루트노드는 따로 부모노드가 없음
for (int i = 2; i <= N; i++) {
if (p[i][j] != -1)
p[i][j + 1] = p[p[i][j]][j];
}
}위 코드로 2^0번째 부모노드 뿐만 아니라, 2^1, 2^2, ... 번째 부모노드와 매핑해줄 수 있다.
이 때, SIZE는 노드개수(N)보다 큰 최소의 2의제곱꼴의 2배로 설정해주었다.
마치, 세그먼트트리의 최소배열의 크기를 설정해줄 때처럼 말이다.
// lca를 구하는 코드 O(lgN)
int lca(int a, int b) {
// 리프노드에 가까운 노드만 조작하기 위해
if (d[a] < d[b])
swap(a, b);
// 두 노드의 높이 차이
int diff = d[a] - d[b];
int j = 0;
// O(lgN)인 이유_ bitmask 개념으로 접근하자
while (diff) {
if (diff % 2)
a = p[a][j];
diff /= 2;
j++;
}
if (a == b)
return a;
// 최악의 경우 루트노드까지 살펴봐야 하므로 SIZE부터 시작
for (int j = SIZE; j >= 0; j--) {
// 두 노드가 같아질 때까지 계속 반복 (한 칸만 더 이동하면 lca가 될 때까지)
if (p[a][j] != -1 && p[a][j] != p[b][j]) {
a = p[a][j];
b = p[b][j];
}
}
// 한 칸 더 올려줘야 lca
a = p[a][0];
return a;
}위 코드로 LCA를 구할 수 있다.
while문 부분과 그 아래 for문 부분을 잘 봐야 한다. LCA를 O(lgN)으로 구해줄 수 있는 부분이다.
두 노드의 높이가 같아질 때까지, 더 깊게 박혀있는 노드를 위로 꺼내준다.
만약 높이차가 11이라고 하자. A가 B보다 더 깊이 박혀있다.
O(N)인 경우는 dfs를 돌아 11번 이동하면서 두 노드 높이를 같게 만들겠지만, 여기서는 11=2^3+2^1+2^0. 총 3번 움직이는 것이다. 비트마스크 개념으로 접근하면 편하다. 따라서 if(diff%2)가 아닌 if(diff&1), diff>>1 와 같이 비트마스크 개념을 도입하여 코드를 작성해도 된다.
for문 부분 또한 우리가 앞에서 구해놓은 부모노드의 정보를 이용하여 O(lgN)으로 lca를 구하게 해준다.
두 노드의 높이가 같아졌다면 이제 본격적으로 lca를 향해 달려갈 차례이다.
이 때도 비트마스크 개념을 이용하면 편하다. lca와 두 노드의 높이의 높이차가 11이라 하자.
for문에서 SIZE부터 거꾸로 살펴보는 이유가 lca보다 높은 부모노드로 접근하는 것을 방지하기 위해서이다. 11=1011(2)이므로 j=4일 때는 p[a][j]가 -1이어서 조건을 만족하지 않게 하고, j=3일 때 조건 만족, j=2일 때 p[a][j]는 2^3+2^2=12번째 노드를 가리키게 되므로 -1이어서 조건불만족. 이런 식으로 해서 lca를 찾아가는 것이다.
해설
쿼리문은 아래와 같다.
- 1 u v: u에서 v로 가는 경로의 비용을 출력한다.
- 2 u v k: u에서 v로 가는 경로에 존재하는 정점 중에서 k번째 정점을 출력한다. k는 u에서 v로 가는 경로에 포함된 정점의 수보다 작거나 같다.
1번은 그냥 경로의 비용을 출력하면 된다. 따라서 (루트-A번 노드의 거리)+(루트-B번 노드의 거리)-2*(루트-lca의 거리)를 해주면 된다. (루트-lca의 거리)가 (루트-A), (루트-B) 거리를 더하면서 두번이나 더해져버렸기 때문이다.
1번 쿼리에서 막혔다면 아래 문제로 더 공부해보고 오자. 1번 쿼리만 있는 LCA 문제이다.
https://www.acmicpc.net/problem/1761
1761번: 정점들의 거리
첫째 줄에 노드의 개수 N이 입력되고 다음 N-1개의 줄에 트리 상에 연결된 두 점과 거리를 입력받는다. 그 다음 줄에 M이 주어지고, 다음 M개의 줄에 거리를 알고 싶은 노드 쌍이 한 줄에 한 쌍씩
www.acmicpc.net
2번 쿼리가 문제인데, A-lca에 해당하는 노드인지, lca를 넘어서 B에 가는 중간에 해당하는 노드인지에 따라 코드가 달라진다.
LCA를 구할 때 2의 제곱꼴번 건너뛰던 것처럼 여기서도 그렇게 하면 된다.
K가 lca-B 중간에 해당하는 경우라면, 먼저 K의 값을 (A-lca)거리만큼 빼준다. 남은 K의 값은 (lca-B)-(B-K번째 노드)가 된다. 주의할 점은, K가 1일 경우 자기 자신이기 때문에 맨처음에 K에서 1을 빼주어야 한다.
cin >> k;
k--;
// A-lca(pnode)에 있는 경우
if (d[a] - d[pnode] >= k) {
for (int i = 0; k > 0; i++) {
if (k % 2)
a = p[a][i];
k /= 2;
}
cout << a << "\n";
}
// lca(pnode)-B에 있는 경우
else {
k -= d[a] - d[pnode];
k = d[b] - d[pnode] - k;
for (int i = 0; k > 0; i++) {
if (k % 2)
b = p[b][i];
k /= 2;
}
cout << b << "\n";
}위와 같이 코드를 작성해주면 된다. 물론 비트마스크 개념을 도입하여 코드를 작성하여도 된다.
코드
// 210615 #13511 트리와쿼리2 Platinum III
// LCA
#include <iostream>
#include <algorithm>
#include <string>
#include <stack>
#include <queue>
#include <vector>
#include <cstring>
#define all(v) (v).begin(), (v).end()
#define press(v) (v).erase(unique(all(v)), (v).end())
using namespace std;
typedef long long ll;
typedef pair<int, int> pi;
typedef pair<ll, ll> pl;
const int SIZE = 17;
const int MAX = 100001;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
int N, M, d[MAX], p[MAX][SIZE + 1];
ll len[MAX];
vector<pi> v[MAX];
void init(int cur) {
for (auto i : v[cur]) {
if (d[i.second] == -1) {
d[i.second] = d[cur] + 1;
len[i.second] = len[cur] + i.first;
p[i.second][0] = cur;
init(i.second);
}
}
}
int lca(int a, int b) {
if (d[a] < d[b])
swap(a, b);
int diff = d[a] - d[b];
int j = 0;
while (diff) {
if (diff % 2)
a = p[a][j];
diff /= 2;
j++;
}
if (a == b)
return a;
for (int j = SIZE; j >= 0; j--) {
if (p[a][j] != -1 && p[a][j] != p[b][j]) {
a = p[a][j];
b = p[b][j];
}
}
a = p[a][0];
return a;
}
int main() {
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(false);
cin >> N;
for (int i = 0; i < N-1; i++) {
int a, b, cost;
cin >> a >> b >> cost;
v[a].push_back({ cost, b });
v[b].push_back({ cost, a });
}
memset(p, -1, sizeof(p));
fill(d, d + MAX, -1);
d[1] = 0;
init(1);
for (int j = 0; j < SIZE; j++) {
for (int i = 2; i <= N; i++) {
if (p[i][j] != -1)
p[i][j + 1] = p[p[i][j]][j];
}
}
cin >> M;
while (M--) {
int ch, a, b, k;
cin >> ch >> a >> b;
int pnode = lca(a, b);
if (ch == 1) {
cout << len[a] + len[b] - 2 * len[pnode] << "\n";
}
else {
cin >> k;
k--;
if (d[a] - d[pnode] >= k) {
for (int i = 0; k > 0; i++) {
if (k % 2)
a = p[a][i];
k /= 2;
}
cout << a << "\n";
}
else {
k -= d[a] - d[pnode];
k = d[b] - d[pnode] - k;
for (int i = 0; k > 0; i++) {
if (k % 2)
b = p[b][i];
k /= 2;
}
cout << b << "\n";
}
}
}
}
'PS > BOJ' 카테고리의 다른 글
| [BOJ] 백준 16132. 그룹 나누기 (Subset) (Gold III) (0) | 2021.07.01 |
|---|---|
| [BOJ] 백준 1348. 주차장 (Platinum II) (0) | 2021.06.21 |
| [BOJ] 백준 15824. 너 봄에는 캡사이신이 맛있단다 (Gold I) (0) | 2021.06.09 |
| [BOJ] 백준 20927. Degree Bounded Minimum Spanning Tree (Gold I) (0) | 2021.06.05 |
| [BOJ] 백준 17616. 등수 찾기 (Gold III) (0) | 2021.05.22 |