그래프 탐색 유형을 연습하기 위해 찾던 중 발견한 문제이다.
KOI 2019 2차대회 초등부 3번 문제이다.
진짜 초등학생들 대단한 것 같다..
https://www.acmicpc.net/problem/17616
17616번: 등수 찾기
표준 입력으로 다음 정보가 주어진다. 첫 번째 줄에 세 정수 N, M, X가 공백을 사이에 두고 주어진다. (2 ≤ N ≤ 105, 1 ≤ M ≤ min(N(N-1)/2, 5×105), 1 ≤ X ≤ N) . 다음 M 줄에는 각각 두 정수 A, B가 주어
www.acmicpc.net

처음에는 위상정렬 + 유니온파인드로 접근하다가,
연결된 컴포넌트들 중 X가 포함이 안된 컴포넌트쪽과 등수비교가 불가능함을 깨닫고 dfs로 바꿔 생각하여 해결한 문제이다.
시행착오
처음에는 위상정렬이 생각나 queue를 이용한 위상정렬로 접근하려 하였다.
X가 포함되지 않은 아예 다른 컴포넌트는 나보다 전부 잘하거나, 나보다 전부 못하는 것으로 간주하여 해결하려 하였다.
문제는 아래와 같은 테스트케이스이다.
10 7 5
1 2
2 3
4 5
5 8
5 9
4 6
6 7
ans: 2 8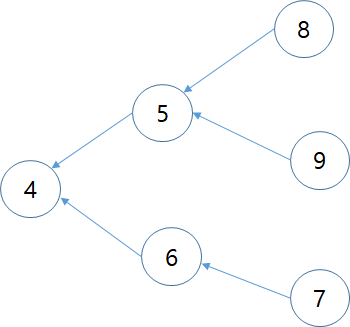
위상정렬로 접근할 경우, 5와 6은 같은 indegree 차수를 가지고 있기 때문에, 등수를 비교할 수 없다.
그러나 이런 차수가 같은 경우는
가장 잘할 때의 등수를 구할 땐, 5가 6보다 잘하는걸로,
가장 못한 때의 등수를 구할 땐, 5가 6보다 못하는 것으로 하면 되기 때문에 문제되지 않는다.
그러나 문제는 5와 7 사이 관계이다.
분명 5와 7은 같은 컴포넌트에 위치하고, 7이 5보다 indegree가 작음이 자명하다.
그러나 가장 못한 때의 등수를 구하려 하면 5는 7보다 못하는 경우로 구해야 한다.
이는 5와 7이 같은 branch에 있지 않기 때문에 그런 것이다.
위상정렬과 다른 조건을 추가하여 구현적으로 잘 이용하여 해결할 수 있는진 모르겠지만,
잘 생각이 나지 않았다.
애초에 위상정렬 문제는 대부분 순서를 나열하고, 답이 여러개인 경우 스페셜저지가 들어가기 때문에 위와 같이 다른 branch임을 확인하여 등수를 가르기에는 적절하지 않다고 생각하여 다른 방법을 찾아보았다.
의식의 흐름 및 해설
잘 생각해보면, X를 기준으로 자신보다 확실하게 뒷등수인 애들, 자신보다 확실하게 앞등수인 애들을 제외하고는 이랬다 저랬다 해도 상관없는 애들이다.
따라서 인접리스트를 두 개를 만들어준다.
while (M--) {
int a, b;
cin >> a >> b;
v[0][b].push_back(a);
v[1][a].push_back(b);
}그리고 DFS를 잘 돌려 자신의 서브트리에 몇 개의 노드가 있는지 파악하면 된다.
서브트리에 있는 노드의 개수는 Gold V급으로 쉬운 수준이므로 누구나 잘 할 수 있을 것이라 본다.
생각을 바꾸니 이렇게 쉬워진다니... 위상정렬로 접근하려다가 피봤다.
코드
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
typedef pair<int, int> pi;
const int MAX = 100001;
const int INF = 0x3f3f3f3f;
int N, M, X;
vector<int> v[2][MAX];
bool visit[MAX];
int dfs(int cur, int type) {
int ret = 1;
visit[cur] = true;
for (auto i : v[type][cur]) {
if (!visit[i])
ret += dfs(i, type);
}
return ret;
}
int main() {
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(false);
cin >> N >> M >> X;
while (M--) {
int a, b;
cin >> a >> b;
v[0][b].push_back(a);
v[1][a].push_back(b);
}
int ans1 = dfs(X, 0);
memset(visit, false, sizeof(visit));
int ans2 = N - dfs(X, 1) + 1;
cout << ans1 << " " << ans2 << "\n";
}사실 visit배열을 따로 memset으로 초기화시켜줄 필요도 없는게, 뒷등수 노드와 앞등수 노드들은 완전 다른 노드들임이 자명하므로 초기화해줄 필요도 없었다.
DFS를 이용한 그래프탐색 문제 많이많이 연습해서
어서 고수가 되고싶다
'PS > BOJ' 카테고리의 다른 글
| [BOJ] 백준 15824. 너 봄에는 캡사이신이 맛있단다 (Gold I) (0) | 2021.06.09 |
|---|---|
| [BOJ] 백준 20927. Degree Bounded Minimum Spanning Tree (Gold I) (0) | 2021.06.05 |
| [BOJ] 백준 1311. 할 일 정하기 1 (Gold I) (0) | 2021.05.20 |
| [BOJ] 백준 3037. 혼란 (Gold I) (0) | 2021.05.19 |
| [BOJ] 백준 17469. 트리의 색깔과 쿼리 (Platinum III) + Set, Map 차이점 및 사용법 (0) | 2021.05.16 |