solvedac 빼빼로 이벤트 중, 막대과자가 부족해서 골드 문제 아무거나 랜덤으로 뽑아서 풀게 된 문제.
문제는 아래와 같다.
https://www.acmicpc.net/problem/22863
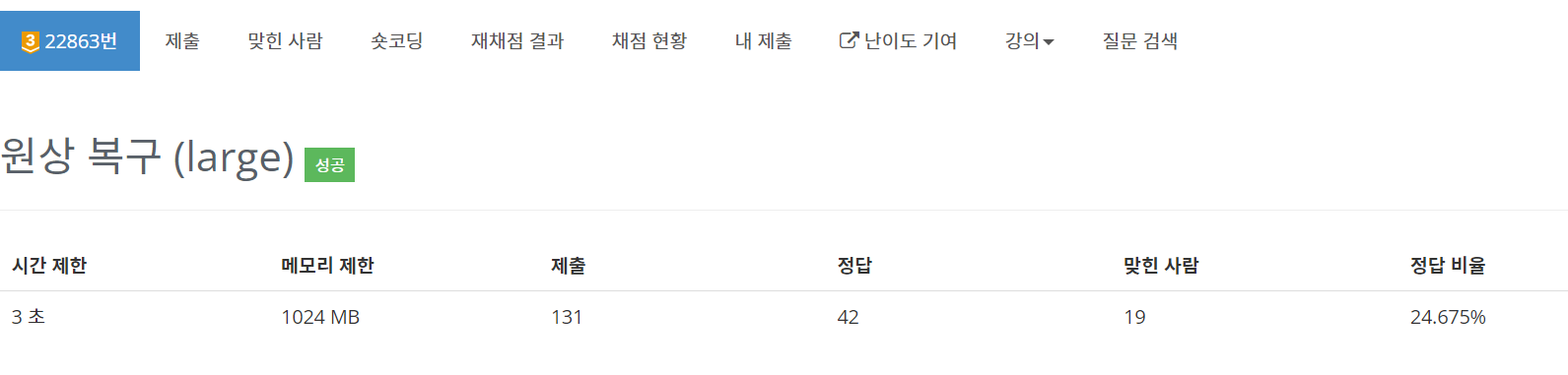
22863번: 원상 복구 (large)
수가 적혀있는 $P_1, P_2, ..., P_N$ $N$개의 카드가 있다. 1부터 N까지 수가 하나씩 존재하는 $D_1, D_2, ... , D_i , ... D_N$ 가 있다. 이때 $D_i$는 $P_{D_i}$ 값을 $i$ 번째로 가지고 오는 것을 의미한다. 이러한
www.acmicpc.net
의식의 흐름 및 해설
문제가 정말 permutation_cycle(순열사이클)처럼 생겼다.
근데 K가 최대 1e15니까 K번 순열 사이클을 돌리는 단순한 풀이는 안되겠다.
순열 사이클은 O(N)에 구할 수 있지만, 순열 사이클의 주기는 사이클들의 주기가 모두 소수일 경우, 주기들의 최소공배수는 어마어마하게 커질 수 있기 때문에 순열 사이클로는 못하겠다!
(아니다... 순열 사이클 분할 풀이로 할 수 있다... 그 때 당시 생각을 못했던 것 뿐이다.)
이거, 쉽지 않은 문젠가 보네 ㅎㅎ
가만, 그러면 lca처럼 비트마스킹으로 logN번 이동할 수 있도록 최적화해주면 되겠다! 그렇게 하면 O(NlgK)의 시간복잡도로 해결할 수 있을테니 말이다.
순열 사이클 분할인 척 하는 sparse table 문제였구만.
그리고 이 문제는 원래 순열을 구하는 문제이기 때문에 역함수를 저장해둬야겠다.
sparse table 풀이가 왜 시간초과지? (사실 지금도 모르겠어서 질문게시판에 글을 남겨두었다. https://www.acmicpc.net/board/view/77875)
(그리고 sparse table 풀이를 최적화하면 통과되긴 한다.)
순열 사이클로 접근해봐야겠다.
잘 생각해보면 모든 순열사이클의 공통주기를 구할 필요 없이,
특정 사이클 주기만으로 답을 충분히 구할 수 있다.
생각해보면 특정 사이클 주기는 최대 N에 불과하기 때문에,
적절한 주기성을 통해 %연산자를 이용하여 K번 이후에 어떤 value를 갖게될 지 파악할 수 있다.
아래 코드의 주석을 보면 이해가 쉬울 것이다.
// 순열 사이클 구하기
for(int j=i;!vis[j];j=d[j]){
vis[j]=true;
// 순열 사이클 index에 따른 value값 구하기 (dictionary를 구한다고 생각하자)
order[cnt++]=j;
}
for(ll j=0;j<cnt;j++){
// 현재 순서에 해당되는 인덱스를 구해주기 위해서
int cur=p[order[j]];
// K번 후 나오는 value
ll idx=order[(j+k)%cnt];
// 문제에서 구하는 것이 원래 순열을 구하는 것이므로 역함수 처리해주자.
res[idx]=cur;
}시간복잡도는 O(N^2)이 아닌 O(N)이다.
순열 사이클을 구할 때, 이미 탐색이 완료된 사이클의 노드라면 continue해주기 때문이다.
순열 사이클로 구하면 굉장히 빠른 시간에 구할 수 있다.
Sparse Table로는 못풀까?
최적화를 굉장히 잘해주면 매우 아슬아슬하게 통과한다.
1. K>=2^j인지 체크할 때, >=보다 빠른 & 연산자를 이용하자.
for(int i=1;i<=n;i++){
ll num=k;
int now=i;
for(int j=50;j>=0;j--){
if(num&1LL<<j){
now=dp[j][now];
}
}
ans[now]=p[i];
}2. sparse table의 꼴을 table[MAXN][50]으로 하지 말고 table[N][MAXN]으로 하자.
이게 왜 더 빠른지는 모르겠다. 그래서 위의 질문게시판에 글을 써놨다.
3. 문제에서 Di가 사실상 sparse table에서의 i번째 value값이 1<<0번째 이동했을 때의 value값이다.
따라서 아래와 같이 코드를 짜주자.
for(int i=1;i<=n;i++)cin>>p[i];
for(int i=1;i<=n;i++)cin>>dp[0][i];
for(int i=1;i<50;i++){
for(int j=1;j<=n;j++){
dp[i][j]=dp[i-1][dp[i-1][j]];
}
}위와 같이 하면 2944ms의 아주아주 아슬아슬한 시간대로 통과가 된다.
O(NlgK)를 막고 O(N)코드만 통과시킬려고 작정하신 것 같기도 하다 ㅜㅜ
코드
순열 사이클 분할(336ms)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX=1000011;
int d[MAX],p[MAX],order[MAX],res[MAX];
ll n,k,t;
bool vis[MAX];
int main() {
cin.tie(0)->sync_with_stdio(0);
cin>>n>>k;
for(int i=1;i<=n;i++)cin>>p[i];
for(int i=1;i<=n;i++)cin>>d[i];
for(int i=1;i<=n;i++){
//dp[d[i]][0]=i;
}
for(int i=1;i<=n;i++){
if(vis[i])continue;
ll cnt=0;
for(int j=i;!vis[j];j=d[j]){
vis[j]=true;
order[cnt++]=j;
}
for(ll j=0;j<cnt;j++){
int cur=p[order[j]];
ll idx=order[(j+k)%cnt];
res[idx]=cur;
}
}
for(int i=1;i<=n;i++)cout<<res[i]<<" ";
}sparse table (2944ms)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX=1000011;
int p[MAX],dp[50][MAX],ans[MAX];
ll n,k,t;
int main() {
cin.tie(0)->sync_with_stdio(0);
cin>>n>>k;
for(int i=1;i<=n;i++)cin>>p[i];
for(int i=1;i<=n;i++)cin>>dp[0][i];
for(int i=1;i<50;i++){
for(int j=1;j<=n;j++){
dp[i][j]=dp[i-1][dp[i-1][j]];
}
}
for(int i=1;i<=n;i++){
ll num=k;
int now=i;
for(int j=50;j>=0;j--){
if(num&1LL<<j){
now=dp[j][now];
}
}
ans[now]=p[i];
}
for(int i=1;i<=n;i++)cout<<ans[i]<<" ";
}
오랜만에 sparse table을 연습하기도 했고,
순열 사이클 분할 응용문제로 색다른 관점을 가져갔기 때문에 많이 배운 듯해서 재밌었던 문제.
다만 최적화가 좀 빡세게 요구돼서 스트레스를 많이 받기도 했다 ㅜㅜ
'PS > BOJ' 카테고리의 다른 글
| [BOJ] 백준 2311. 왕복 여행 (Platinum II) (0) | 2021.11.18 |
|---|---|
| [BOJ] 백준 14950. 정복자 (Gold III) (0) | 2021.11.11 |
| [BOJ] 백준 10167. 금광 (Diamond V) (0) | 2021.11.04 |
| [BOJ] 백준 20553. 다오와 디지니의 데이트 (Gold II) (0) | 2021.10.31 |
| [BOJ] 백준 2487. 섞기 수열 (Gold IV) (0) | 2021.10.29 |