2009 KOI 고등부 1번 문제이다.
문제는 아래와 같다.
https://www.acmicpc.net/problem/2487
2487번: 섞기 수열
A1, A2, …, AN으로 표시된 N 개의 카드를 정해진 방법으로 섞고자 한다. 그 섞는 방법은 1에서 N까지의 숫자로 이루어진 수열로 표시된다. 이 수열을 섞기 수열이라 하자. 섞기는 현재 가지고 있는
www.acmicpc.net
문제를 요약하자면,
섞기 전 index에 위치한 value값을 섞은 후의 index로 위치하게 할 때,
맨 처음 순서와 똑같은 순서로 놓이게 되는 때는 몇 번째인지 구하는 문제이다.
의식의 흐름 및 해설
섞기 전 index에 위치한 value가 섞은 후에는 index에 위치하게 된다.
이를 그림으로 나타내면 아래와 같다.
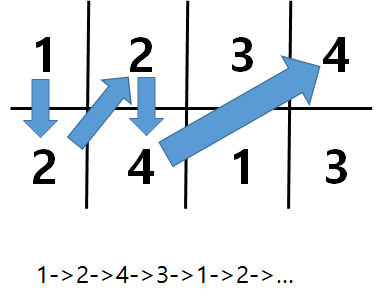
위 그림을 예로 들면,
처음 섞을 때는 2, 4, 1, 3이 되고,
이후에는 4, 3, 2, 1이 되고,
이후에는 1, 2, 3, 4이 된다.
첫 번째 원소는 1->2->4->3->1
두 번째 원소는 2->4->3->1->2
세 번째 원소는 3->1->2->4->3
네 번째 원소는 4->3->1->2->4 가 됨을 확인할 수 있다.
따라서 위 그림 예시의 답은 4이다. 4번만에 원래대로 돌아옴을 알 수 있다.
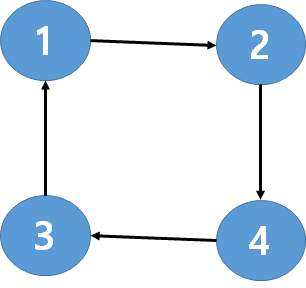
따라서 우리는 위 순열을 그래프로 나타내 사이클의 주기를 파악해야한다는 사실을 알 수 있다.
순열 사이클들이 그림 예시에선 하나 뿐이지만,
예제에선 두 개 이상이므로, 순열 사이클들의 최소공배수가 답이 된다.
for(int j=i;!vis[j];j=A[j]){
vis[j]=true;
cnt++;
}vis 변수가 true인 게 나올 경우, 이미 방문한 노드이므로
순열 사이클임이 확인된다.
따라서 for문 조건을 위와 같이 걸고, cnt가 사이클의 주기가 됨을 확인할 수 있다.
사이클이 여러개라면, cnt끼리의 최소공배수를 구해주면 된다.
이 때, 유클리드 호제법으로 시간을 절약해주자.
코드
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,A[20011];
ll ans=1;
bool vis[20011];
ll gcd(ll a,ll b){
ll r=a%b;
if(!r)return b;
return gcd(b,r);
}
void solve(){
for(int i=1;i<=n;i++){
if(!vis[i]){
ll cnt=0;
for(int j=i;!vis[j];j=A[j]){
vis[j]=true;
cnt++;
}
ans=ans*cnt/gcd(ans,cnt);
}
}
}
int main() {
cin.tie(0)->sync_with_stdio(0);
cin>>n;
for(int i=1;i<=n;i++){
cin>>A[i];
}
solve();
cout<<ans;
}사실 이 문제는 어떤 그리디문제를 풀려다가
뭔가 원하는대로 잘 풀리지 않아 공부한 문제이다.
그 그리디 문제를 풀게 될 때까지 꾸준히 공부하고, 풀게 될 경우 포스팅하겠다.
'PS > BOJ' 카테고리의 다른 글
| [BOJ] 백준 10167. 금광 (Diamond V) (0) | 2021.11.04 |
|---|---|
| [BOJ] 백준 20553. 다오와 디지니의 데이트 (Gold II) (0) | 2021.10.31 |
| [BOJ] 백준 11406. 책 구매하기2 (Platinum IV) + Dinic(디닉) Algorithm (0) | 2021.10.27 |
| [BOJ] 백준 17612. 쇼핑몰 (Gold I) (0) | 2021.10.24 |
| [BOJ] 백준 4225. 쓰레기 슈트 (Platinum III) (0) | 2021.10.24 |