요즘 백준 풀문제들, 공부할 내용들이 많다보니 알고리즘 공부 우선순위가 상당히 높아져있다.
포스팅도 대부분 백준 관련 포스팅으로 이루어져버렸다.
아무튼 문제는 아래와 같다.
https://www.acmicpc.net/problem/13710
13710번: XOR 합 3
첫째 줄에는 배열의 크기 N (1 ≤ N ≤ 100,000), 둘째 줄에는 수열 A에 들어있는 수가 주어진다. 수열 A에 들어있는 수는 109보다 작거나 같은 음이 아닌 정수이다.
www.acmicpc.net
의식의 흐름 및 해설
처음엔 좀 쉬운 문제가 아닌가 생각했다.
수열 a1, a2, ... , an이 있을 때, 연속하는 부분수열의 xor합을 구하기 위해선 누적합으로 p[i-1]^a[i]+a[i]를 해주면 되지 않나 싶어서 간단하게 아래 코드로 제출했다.
for(int i=1;i<=n;i++){
cin>>k;
// 처음엔 p[i]=a[i]
if(i==1)
p[i]=k;
// 그 다음부턴 p[i]=p[i-1]^a[i]+a[i]
// (a[1]+...+a[i-1])^a[i] + a[i]
else
p[i]=(p[i-1]^k)+k;
ans+=p[i];
}
cout<<ans;그러나 뜨는 결과는 바로 '틀렸습니다'.
이유가 뭘까 생각해보니 xor은 분배법칙이 성립하지 않는다.
생각해보면 당연하다. 덧셈은 자릿수가 올라가버리는데, xor은 1이 두개일 경우 0으로 되어버리기 때문이다.
우선 xor의 성질을 잘 생각해보자.
수열 중 구간 [L, R]에 해당하는 부분수열의 xor합은 아래와 같다.
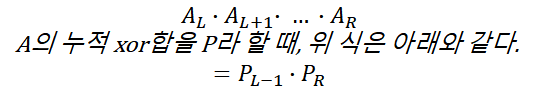
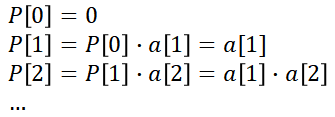
편의상 xor을 점자로 찍었다. (사실 xor 기호를 못찾겠다.)
위 식이 성립하는 이유는 같은 수를 두 번 xor하면 0이 되는 성질이 있기 때문이다.
따라서 우리는 식을 아래와 같이 정리할 수 있다.
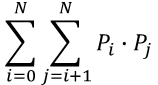
그러나 위 식 또한 O(N^2)으로 보인다.
어떻게 시간복잡도를 줄일 수 있을까?
O(N(lg10억))만에 풀 수 있는 방법이 있다.
바로 수의 범위가 1e9까지이므로 2^30까지임을 고려하면 된다.
이제 아래 문제에서 활용되는 풀이를 이용하면 된다.
i번째 비트가 1일 때 수가 증가하므로, i번째 비트가 0인 개수 * i번째 비트가 1인 개수 * (1LL<<i)를 답에 더해주면 된다.
https://www.acmicpc.net/problem/2830
2830번: 행성 X3
상근이는 초등학교 졸업 여행으로 외계 행성 X3에 방문했었다. 이 행성에 사는 사람들의 이름은 모두 자연수이다. 행성의 거주민은 모두 서로를 알고 있다. 두 X3인은 그들의 친밀도를 자신의 이
www.acmicpc.net
코드
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int MAX=100011;
int N;
ll cnt[30][2], a[MAX], p[MAX];
int main() {
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(false);
cin>>N;
for(int i=1;i<=N;i++){
cin>>a[i];
p[i]=p[i-1]^a[i];
}
for(int i=0;i<=N;i++){
for(int j=0;j<30;j++){
cnt[j][(bool)(p[i]&(1<<j))]++;
}
}
ll ans=0;
for(int i=0;i<30;i++){
ans+=cnt[i][0]*cnt[i][1]*(1LL<<i);
}
cout<<ans<<"\n";
}시간이 별로 없어서 마지막에 글을 좀 대충 썼는데, 나중에 시간되면 보강해야겠다.
'PS > BOJ' 카테고리의 다른 글
| [BOJ] 백준 17612. 쇼핑몰 (Gold I) (0) | 2021.10.24 |
|---|---|
| [BOJ] 백준 4225. 쓰레기 슈트 (Platinum III) (0) | 2021.10.24 |
| [BOJ] 백준 11014, 1014. 컨닝 2 (Platinum II) (0) | 2021.10.17 |
| [BOJ] 백준 1867. 돌멩이 제거 (Platinum III) (0) | 2021.10.17 |
| [BOJ] 백준 1990. 소수인팰린드롬 (Gold V) (0) | 2021.10.17 |