flow 이론에 있어서 나름 구현은 쉽지만 중요한 문제이다.
문제는 아래와 같다.
https://www.acmicpc.net/problem/1867
1867번: 돌멩이 제거
첫째 줄에 n과 k가 주어진다. (1 ≤ n ≤ 500, 1 ≤ k ≤ 10,000) 이후 k개의 줄에는 돌멩이의 위치가 한 줄에 하나씩 주어진다. 줄마다 첫 번째 숫자는 행 번호, 두 번째 숫자는 열 번호를 나타낸다.
www.acmicpc.net
의식의 흐름 및 해설
특정 행, 열을 최소한으로 선택하여 모든 돌멩이를 제거하는 문제이다.
행을 선택하면 그 행에 포함된 돌멩이의 열들이 영향을 받는다.
단, 다른 행들은 영향을 받지 않는다.
따라서 행과 열로 이분그래프를 나눠볼 수 있다.
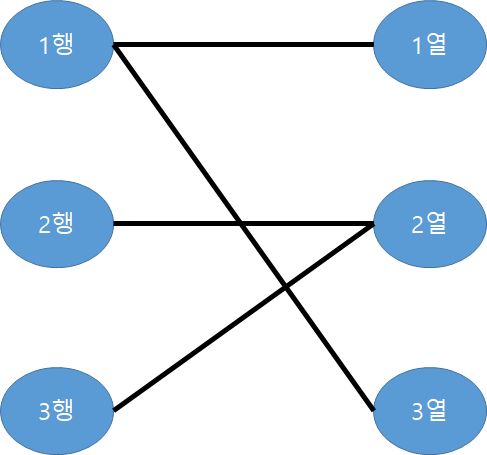
여기서 돌멩이는 행-열을 연결하는 간선을 의미한다고 생각할 수 있다.
즉, 위 그림에서 모든 간선을 포함하는 최소 버텍스 커버(Minimum Vertex Cover) 문제로 바꿔 생각할 수 있다는 것이다.
퀴닉의 이론(konig's theorem)에 의해 아래 성질이 성립한다.
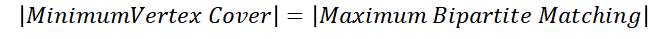
따라서 이 문제는 이분매칭 문제로 바뀌게 된다.
최대 매칭을 구해주자.
코드
#include <iostream>
#include <algorithm>
#include <string>
#include <vector>
#include <cstring>
#include <queue>
#include <cmath>
#include <stack>
#include <set>
#include <map>
#define all(v) (v).begin(), (v).end()
#define press(v) (v).erase(unique(all(v)), (v).end())
using namespace std;
typedef long long ll;
typedef pair<int, int> pi;
typedef pair<int, pi> pii;
const int MAX = 503;
const int INF = 0x3f3f3f3f;
const int LNF = 1e18;
const int MOD = 1e9 + 7;
int N, K, ans, d[MAX];
vector<int> v[MAX];
bool used[MAX];
bool dfs(int cur) {
for (auto i : v[cur]) {
if (used[i])
continue;
used[i] = true;
if (d[i] == -1 || dfs(d[i])) {
d[i] = cur;
return true;
}
}
return false;
}
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> N >> K;
for (int i = 0; i < K; i++) {
int a, b;
cin >> a >> b;
v[a].push_back(b);
}
memset(d, -1, sizeof(d));
for (int i = 1; i <= N; i++) {
fill(used, used + MAX, false);
if (dfs(i))
ans++;
}
cout << ans << "\n";
}만약 어떤 행과 열을 선택해야하는지 구해야 된다면?
이분매칭으로 값은 구했지만, 어떤 행과 열을 선택해야하는지는 이분매칭으로 매칭된 vertex와 minimum vertex cover의 vertex들이 같지 않다.
어떤 행과 열을 선택해야하는지 구하려면 minimum vertex cover의 정의를 이용하여 추가적인 작업을 해주어야한다.
Source와 연결된 vertex의 집합을 L,
Sink와 연결된 vertex의 집합을 R이라 하자.
L에서 매칭되지 않은 vertex의 집합을 matching(alternating path을 통해 방문가능한 집합)한 R의 vertex들을 X,
R에서 매칭되지 않은 vertex의 집합을 matching(alternating path을 통해 방문가능한 집합)한 L의 vertex들을 Y라 하면,
아래의 집합이 답이 된다.
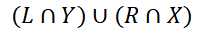
minimum vertex cover도 결국 vertex cover이기 때문에 여기에 포함된 간선들은 minimum vertex cover의 vertex들을 연결해야 하기 때문에 위와 같이 답을 내릴 수 있다.
매칭 관련 그래프 이론은 아래 포스팅에서 공부하였다.
최대 이분 매칭에 관한 몇 가지 정리 - http://www.secmem.org/blog/2019/12/15/theorem-about-bipartite-matching/
디닉 알고리즘 - https://gina65.tistory.com/5
매칭 알고리즘 증명 및 정당성 - https://koosaga.com/18 https://koosaga.com/133
최소 버텍스 커버 포스팅 - https://www.crocus.co.kr/756
유량을 언젠가는 공부해야지... 하다가 그래프 쪽에서 유량 관련 문제들이 꽤나 보여 결국 공부하는 중이다.
알고리즘의 정당성과 증명과정의 중요성을 느껴서 깊게 공부해보고 있는데,
(알고리즘의 증명 및 정당성을 알게 된다면 다양한 응용, 변형문제들을 풀 수 있는 힘을 가지게 된다... 고 생각한다 ㅎㅎ)
깊게 파면 팔수록 어렵고 다양하게 응용될 수 있다는 것에 놀랐다.
사실 예전에 flow쪽을 얕게 파본 적이 있는데, 그 때는 진짜 겉핥기밖에 하지 않았다는 것을 깨닫는다.
'PS > BOJ' 카테고리의 다른 글
| [BOJ] 백준 13710. XOR 합 3 (Gold I) (0) | 2021.10.18 |
|---|---|
| [BOJ] 백준 11014, 1014. 컨닝 2 (Platinum II) (0) | 2021.10.17 |
| [BOJ] 백준 1990. 소수인팰린드롬 (Gold V) (0) | 2021.10.17 |
| [BOJ] 백준 17401. 일하는 세포 (Platinum V) (0) | 2021.10.17 |
| [BOJ] 백준 22345. 누적 거리 (Gold III) (0) | 2021.10.17 |