프로그래머스 월간 코드 챌린지 3번 문제를 풀지 못해
tree + dfs 연습을 좀 더 빡세게 해야겠다 싶어서 선정한 문제들 중 하나이다.
역시나...플레티넘 난이도 답게 굉장히 어려웠다.
20188번: 등산 마니아
동네 뒷 산에는 등산로가 있다. 등산로는 N개의 작은 오두막들이 N −1개의 오솔길로 이어진 형태이다. 한 오솔길은 두 개의 오두막을 양 방향으로 연결한다. 한 오솔길의 길이는 1이다. 어떤 오
www.acmicpc.net
KOI 2020 2차대회 초등부 3번, 중등부 2번 문제이기도 한데,
이거 보면서 진짜 요즘 초등학생, 중학생들은... 정말 대단하다는 생각도 들고,
똑똑한 친구들은 다르구나 생각이 많이 들었다.
개인적으로 친구들이나 아는 사람들한테 이 문제 보여주면서,
'이게 초등부 문제래! 세상에!' 라는 반응을 하고 싶었는데, 주변에 알고리즘 하는 지인이 없어서... 아쉽다.
이문제 포스팅하는 이유는, 아이디어가 신박하기도 하고,
이 문제 아이디어 (관점)과 비슷하기 때문이다.
7812번: 중앙 트리
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫 줄에는 트리의 정점의 수 n이 주어진다. (1 ≤ n ≤ 10,000) 각 정점은 0번부터 n-1번까지 번호가 붙여져 있다. 다음 n-1개 줄
www.acmicpc.net
의식의 흐름 및 해설
일단 딱봐도 문제가 tree + dfs임이 확실해보이지 않는가? (뭐 사실 트리 나오면 거의 dfs니까)
의식의 흐름은 개뿔... LCA 풀이가 O(N^2lgN)으로 시간초과가 예상돼서 머리싸매고 고민하다가 결국 풀이를 참고한 문제이다. 풀이는 이 영상을 참고했다.
www.youtube.com/watch?v=AQzKDzQqIRE
O(N)으로 문제를 해결하게 해주는 놀라운 마법!
바로 트리dp 덕분이다.
서브트리의 크기를 리프노드에서부터 계속 갱신해주기 때문에 트리dp이다.
일단 맨 처음, 내가 생각한 LCA 풀이는 아래와 같다.
- 각각의 (i, j) 쌍에 대해 답을 구해서 ans에 더한다. 이 때, (i, j)쌍이 n(n-1)/2개 나오므로, 시간복잡도는 O(N^2)*답을 구하는 과정의 시간복잡도
- 따라서 (i, j)쌍에 대해서 (i<->lca) + (lca<->j) + (lca<->1) 개로 O(lgN)으로 답을 구해도, (심지어 O(1) lca풀이로 답을 구해도) O(N^2)이므로 시간초과가 난다.
따라서 위 영상에서 설명해준대로 간선의 관점에서 바라보아야 한다.
간선의 관점?? 이게 대체 무슨소리냐?
라고 할까봐 예시를 들어가며 설명할거다.

위와 같이 산이 있다고 하자.
우리가 구하려는 것은 각각의 간선이 총 몇 번 사용되는지의 합을 구하는 것이므로, 아래와 같이 예시를 들어보겠다.
예를 들어 5->6 의 간선이 몇 번 사용되는지 알아보고 싶다.
우린 네 가지 경우로 나눠볼 수 있다.
(여기서 5 또는 5의 서브트리: 6의 서브트리를 제외한 나머지 노드들(5, 7, 1, 4, 3번 노드)을 의미한다!)
1. 출발점이 (5 또는 5의 서브트리), 도착점 또한 (5 또는 5의 서브트리)
2. 출발점이 (5 또는 5의 서브트리), 도착점은 (6 또는 6의 서브트리)
3. 출발점이 (6 또는 6의 서브트리), 도착점은 (5 또는 5의 서브트리)
4. 출발점이 (6 또는 6의 서브트리), 도착점 또한 (6 또는 6의 서브트리)
일단 2, 3번의 경우는 무조건 5->6 간선을 지날 수 밖에 없다.
그럼 남은 건 1, 4번 경우인데,
이 문제는 특이하게도, 정상을 꼭 거친 후 목표노드로 이동해야된다.

따라서 4번의 경우 또한 위와 같은 그림이 나오므로 4번 경우 또한 만족하게 된다.
그럼 1번 경우는 어떨까?
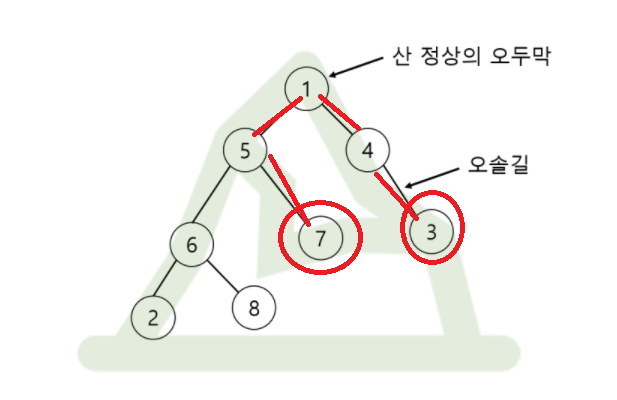
그림으로 보다시피
(필자가 개똥손임을 알 수 있음과 함께) 1번 경우는 5->6 간선에서의 (6번과 6번의 서브트리) 자체로 올 일이 없으므로 포함되지 않는다.
1번 경우는 어떤 경우에도 lca가 5번이거나 5번보다 상위 노드이기 때문이다.

따라서 우린 u, v 간선이 얼마나 사용되는지 알기 위해서는
(전체에서 2개의 노드를 선택하는 경우의 수) - (parent(u, v)를 포함한 subtree의 크기(1번 경우)에서 2개의 노드를 선택하는 경우의 수)
를 해주면 됨을 알 수 있다.
2개를 선택하는 경우의 수는 nC2 = n(n-1)/2임을 이용하면 된다.
이 때, N*(N-1) 과정에서 3e5*3e5 = 9e10이어서 int 범위를 벗어나게 되므로 주의하자.
각각의 간선 N-1개가 얼마나 사용되는지 알려면,
트리를 dfs로 각 간선을 돌면서 각 경우의 parent 노드를 포함한 서브트리의 크기를 제외한 경우의수를 구해주면 된다.
dfs 성질을 생각하면 결국 모든 간선을 1번씩 탐색하는 O(N) 성격을 띄기 때문에
모든 간선에 대한 각각의 답을 구해서 합해주면 된다.
이 때, 1번은 루트노드이므로, 값이 중복돼서 들어감에 유의하자.
코드
#include <iostream>
#include <vector>
#include <algorithm>
#define all(v) (v).begin(), (v).end()
using namespace std;
typedef long long ll;
const int MAX = 300001;
vector<int> v[MAX];
ll N, d[MAX], ans;
ll ret(ll n) {
return n * (n - 1) / 2;
}
ll dfs(int cur) {
d[cur] = 1;
for (auto i : v[cur]) {
if (!d[i]) {
d[cur] += dfs(i);
}
}
ans += ret(N) - ret(N - d[cur]);
return d[cur];
}
int main() {
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(false);
cin >> N;
for (int i = 0; i < N - 1; i++) {
int a, b;
cin >> a >> b;
v[a].push_back(b);
v[b].push_back(a);
}
dfs(1);
cout << ans - ret(N) << "\n";
}
개인적으론 #7812와 난이도가 비슷하다 생각해 Platinum IV 정도의 난이도라 생각한다.
아이디어가 너무 어려워 막상 dfs를 많이 연습한 게 아닌,
또 다른 웰노운의 방법을 익힌 셈인 듯 하지만,
dfs를 다루는 데에 분명히 도움이 됐지 않을까 싶어 만족스러운 문제였다.
재밌기도 하고.
5월까진 골드 트리문제들을 보다 좀 더 집중적으로 풀어봐야겠다.
'PS > BOJ' 카테고리의 다른 글
| [BOJ] 백준 2800. 괄호 제거 (Gold V) (0) | 2021.05.15 |
|---|---|
| [BOJ] 백준 14461. 소가 길을 건너간 이유 7 (Gold II) (0) | 2021.04.23 |
| [BOJ] 백준 20040. 사이클 게임 (Gold IV) (0) | 2021.04.06 |
| [BOJ] 백준 10256. 돌연변이 (Platinum III) (0) | 2021.04.04 |
| [BOJ] 백준 2157. 여행 (Gold IV) (0) | 2021.04.01 |