그룹원 한분께서 요청해주신 문제를 해결하면서 degree sequence 라는 개념을 알게 됐다.
Warming Up
요청해주셨던 문제는 아래와 같다. 한 번 풀어보도록 하자. (degree sequence 개념을 몰라도 해결이 가능하다.)
https://www.acmicpc.net/problem/23578
23578번: 비 오는 날
피에스고등학교의 교장 이환이는 학교를 매우 사랑한다. 그래서 이환이는 매일 점심시간에 학교의 모든 건물을 돌아다닌다. 비가 오는 어느 날, 이환이는 학교 곳곳을 돌아다니고 싶었지만 비
www.acmicpc.net
불만을 최소화하기 위해서는 최소한의 다리로 건물을 연결해야 하며, 따라서 mst를 금방 떠올릴 수 있다.
그러나, 단순 mst 문제는 아니고, 차수에 따라 답이 달라지는 mst이기 때문에 아래 포스팅의 경우를 생각하여 단순그리디 mst로 접근해선 안된다는 것을 캐치했어야 한다.
https://kth990303.tistory.com/69
[BOJ] 백준 20927. Degree Bounded Minimum Spanning Tree (Gold I)
문제는 아래와 같다. https://www.acmicpc.net/problem/20927 20927번: Degree Bounded Minimum Spanning Tree 제약에 맞는 Spanning Tree가 존재한다면 첫 번째 줄에 YES를 출력하여라. 이후 해당 Spanning Tree..
kth990303.tistory.com
만약 캐치하지 못했다면 아래 반례를 통과하지 못할 확률이 높다.
4
3 3 2 2
Ans:22
Wrong:25
위 문제를 해결하지 못해도 괜찮다.
Degree Sequence 개념을 한 번 익혀보고 쉬었다가 해결해보자.
Degree Sequence
구글링해도 자료가 많이 안나와서 아래 영상으로 공부했다.
https://www.youtube.com/watch?v=aNKO4ttWmcU&t=2s
degree sequence란, 그래프에 속해있는 모든 노드의 차수를 수열로 표시한 것을 의미한다.
아래 그래프를 예시로 살펴보자.
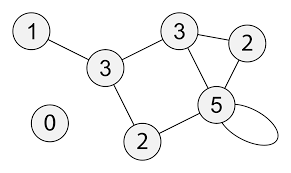
위 사진은 두 개의 컴포넌트로 구성된 그래프이다.
노드 안에 적혀있는 숫자가 각 node의 degree이며,
이를 1번노드부터 차례대로 수열로 나타낸 것을 degree sequence라고 할 수 있다.
이 degree sequence는 의외로 많은 도움을 준다.
degree sequence만으로 이 그래프가 트리인지 아닌지, 어떤 트리 형태를 가지고 있는지, 그래프가 될 수 있는지 없는지를 파악할 수 있다.
주의할 점은, degree sequence가 같다고 해서 반드시 동형사상의 그래프는 아니라는 점이다.

위와 같은 경우만 봐도 차수만으론 그래프를 단정지을 순 없다는 것을 확인할 수 있다.
증명 방법도 있는데, 티스토리로 그래프를 그리기가 상당히 귀찮으니, 위 유튜브 영상을 참고하도록 하자... (죄송합니다 ㅠㅠ)
Degree Sequence로 그래프인지 아닌지 어떻게 파악함?
먼저, 그래프에서의 각 노드들의 차수는 음수가 될 수 없다는 점을 알아두자.
그리고, degree sequence로 파악하기 전에, 각 노드들의 차수의 합이 짝수가 아니라면 애초에 그래프가 될 수 없다.
이는 edge가 두 개의 vertex와 연결되는 것이기 때문이다.
방법은 아래와 같다.
1. Degree Sequence를 내림차순으로 정렬하자.
2. 가장 degree가 큰 D(1)=Value(1)이라고 하자. D(2), D(3), ... , D(1+Value1)과 D(1)을 이어주면, D(1)은 Value(1)개수만큼의 노드와 연결이 됐으므로 차수를 만족한다. 따라서 D(1)은 이제 지워주고, D(2),..., D(1+Value1)에 해당하는 노드들의 value값은 1씩 빼준다. 만약 1씩 뺐을 때 0이 됐다면, 그 노드는 더 이상 연결해줄 필요가 없으므로 지워주자.
3. 이 때 degree sequence를 sequence' 이라 할 때, sequence'으로 그래프임이 자명하면 sequence로도 그래프를 나타낼 수 있다. 만약 자명하지 않다면 1번부터 다시 반복하자.
아마 이해가 잘 안될 것이다.
아래 예시들을 보면서 차근차근 이해해보도록 하자.
Example 1. [1,2,1,2,1,2] degree sequence를 이루는 것은 그래프가 될 수 있을까? (Graphical일까?)
Answer 1. NO
degree들의 합이 even이 아니므로 그래프가 될 수 없다.
degree sequence의 sum of degree가 짝수여야 그래프가 될 자격이라도 갖춘다는 것을 명심하자.
Example 2. [1,2,2,1,2,2] degree sequence를 이루는 것은 그래프가 될 수 있을까? (Graphical일까?)
Answer 2. YES
일단 degree들의 합이 10으로 그래프는 맞을 듯하다. (눈치가 빠른 분들은 트리도 가능하다는 것을 알아챘을 것이다!)
그런데 그래프가 맞을 지는 확신이 서지 않는다.
따라서 위에서 설명한 방법대로 진행해보자.
1. 내림차순 정렬 => [2,2,2,2,1,1]
2. 첫번째 노드를 (맨 첫번째 노드의 차수)만큼 다른 노드들과 연결한다. => [0,1,1,2,1,1]
그리고 첫번째 노드는 0이 됐으므로 지워주자. => [1,1,2,1,1]
3. 그래프임이 자명한가? 난 잘 모르겠다. 다시 반복해주자.
1. 내림차순 정렬 => [2,1,1,1,1]
2. 첫번째 노드를 (맨 첫번째 노드의 차수)만큼 다른 노드들과 연결한다. => [0,0,0,1,1]
그리고 0이 된 노드들은 지워주자. => [1,1]
3. 그래프임이 자명한가? [1,1]은 서로 edge로 연결해주면 만족하기 때문에 그래프임이 자명하다!
따라서 [1,2,2,1,2,2]는 그래프임이 자명하다.
이는 아래 모양과 같다.
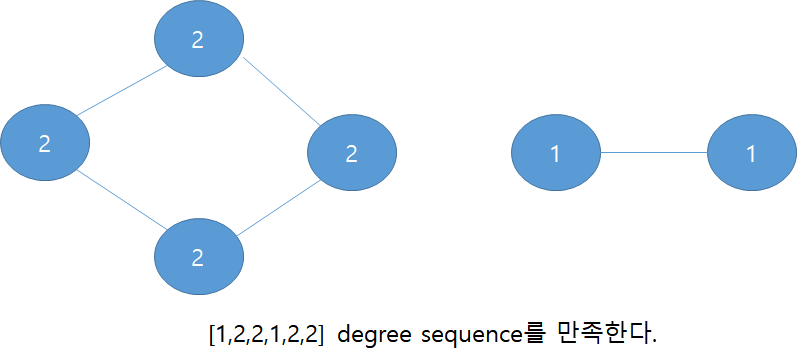
따라서 내림차순 정렬하는 경우가 반복되기 때문에,
보통 degree sequence를 응용하는 문제들은 priority_queue가 많이 사용된다.
이는 가끔씩 어려운 문제에서의 topology_sort 문제들에서 priority_queue가 사용되는 이유이기도 하다.
Degree Sequence로 트리인지도 파악 가능함?
물론이다.
트리의 성질을 잘 생각해보자.
N개의 노드와 N-1개의 edge로 이루어져있다. 따라서 2N-2개의 차수를 가지면 tree이다.
따라서 degree sequence의 합이 2N-2일 경우 트리이다.
근데 graphical한지 먼저 따져야된다고 생각할 수도 있다.
다행히 걱정 안해도 되는게 합이 2N-2일 경우 무조건 graphical이다.
각 차수의 value에 해당하는 만큼 sum(다른 노드들의 차수에서 빼지는 차수의 절댓값)도 value이기 때문에 최대 N-1씩 두 번 빼지기 때문에 무조건 graphical함을 알 수 있다.
연습문제도 있음?
그렇다.
아래 문제를 추천한다.
https://www.acmicpc.net/problem/8286
8286번: Road Network 2
If no road network plan satisfying the conditions from the input exists, the first and only line of output should contain a single word BRAK - i.e., none in Polish. In the opposite case each of the lines in the output should contain a description of one bi
www.acmicpc.net
사실 연습문제 치곤 좀 어려운데,
각 노드들의 degree가 주어질 때, 이를 적절한 트리 형태로 만들 수 있는지 파악하고,
그 형태까지 출력해야되는 문제이다.
만들 수 있을지 파악하는 것은 위에서 설명했기 때문에 쉬울건데, 그 형태를 출력하는 것이 좀 어려울 수 있다.
위에서 언급한대로 priority_queue를 적절히 이용하여 문제를 해결할 수 있다.
사실 내가 기억해두려고 썼기 때문에
엄밀한 증명은 여기서는 생략한데다가, 글 가독성도 좋아보이지 않지만,
없는 것보단 나을 거 같아서 기록해둔다.
그리고 degree sequence는 tree에서 특별한 성질이 하나 더 있는데,
귀차니즘이 풀린다면 언젠가는 포스팅해볼 예정이다.
'PS > Algorithm' 카테고리의 다른 글
| 이분매칭 알고리즘 (feat. Minimum Vertex Cover) (추후 보완 예정) (0) | 2022.04.07 |
|---|---|
| [Knapsack DP] 냅색은 바텀업으로 - 연습문제 유형익히기 (2) | 2021.11.22 |
| [Knapsack] 냅색은 웬만해선 바텀업으로 짜자 (3) | 2021.11.08 |
| Implementation_구현[기초] (Bronze 중위권) (0) | 2021.01.19 |