정말 기가막히도록 대단한 문제라 생각된다.
문제는 아래와 같다.
https://www.acmicpc.net/problem/14574
14574번: 헤븐스 키친
남규는 요즘 군입대를 기다리며 하루 종일 유튜브를 본다. 남규가 가장 좋아하는 채널은 ‘Heaven`s kichen’이다. 이 프로그램에서는 N명의 요리사가 매일 둘씩 요리 대결을 펼치고, 승리한 요리사
www.acmicpc.net
대충 생각나는 건 수학, 그래프 알고리즘이 생각나지 않는가?
좀 더 생각해보면 MST와 dfs로 연결지을 수 있다.
의식의 흐름 및 해설
이긴 사람은 천국으로 떠나고, 진 사람이 경기를 계속해서 이어갈 수 있는 특이한 룰이다.
즉, 사람 수가 N명일 때, 경기는 N-1번 진행된다.
시청률의 합이 최대가 되도록 해야 하며, 이긴 사람이 N-1명이 존재해야 하므로, 경기 대진표를 그려볼 때 트리 모양으로 이루어짐을 확인할 수 있다. 아래 그림을 보자.
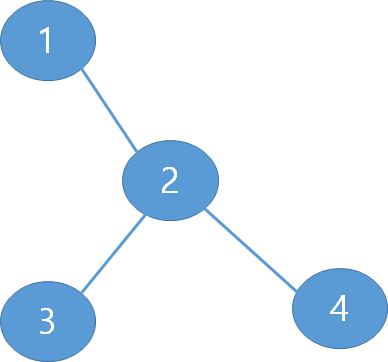
1번과 2번이 경기를 할 때, 1번이 승리하여 천국갔다고 해보자.
그럼 2번은 3번과 경기를 하고, 3번이 승리하여 천국가고, 2-4 경기하는 모습이 나온다.
이렇게 트리 모양으로 N-1개의 경기가 형성됨을 확인할 수 있다.
또한, 모든 사람은 최소 1번 씩 경기를 진행해야 하므로 그리디적으로 MST로 접근할 수 있다.
그리고 문제에서 조금 까다로운 것은 "패자 승자" 형태로 경기진행 역추적을 이용해 출력해주어야 한다는 점이다.
이 부분은 DFS로 처리할 수 있다.
DFS는 재귀적으로 리프노드까지 탐색하며, 리프노드는 하나의 간선으로만 연결돼있기 때문에 승자, 부모노드는 패자로 연결지으면 된다.
코드
#include <iostream>
#include <algorithm>
#include <string>
#include <vector>
#include <cstring>
#include <queue>
#include <cmath>
#include <stack>
#include <set>
#include <map>
#define all(v) (v).begin(), (v).end()
#define press(v) (v).erase(unique(all(v)), (v).end())
using namespace std;
typedef long long ll;
typedef pair<int, int> pi;
typedef pair<int, pi> pii;
const int MAX = 500001;
const int INF = 0x3f3f3f3f;
int N, p[MAX];
vector<int> res[MAX];
vector<pi> c;
vector<pii> v;
int find(int a) {
if (a == p[a])
return a;
return p[a] = find(p[a]);
}
bool merge(int a, int b) {
a = find(a);
b = find(b);
if (a == b)
return false;
if (a > b)
swap(a, b);
p[b] = a;
return true;
}
void trace(int cur, int prev) {
for (auto i : res[cur]) {
if (i == prev)
continue;
trace(i, cur);
}
if (prev != -1)
cout << prev + 1 << " " << cur + 1 << "\n";
}
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> N;
c.resize(N);
for (int i = 0; i < N; i++) {
p[i] = i;
cin >> c[i].first >> c[i].second;
}
for (int i = 0; i < N; i++) {
for (int j = i + 1; j < N; j++) {
int n = (c[i].second + c[j].second) / abs(c[i].first - c[j].first);
v.push_back({ n, {i, j} });
}
}
sort(all(v));
reverse(all(v));
ll ans = 0;
for (int i = 0; i < v.size(); i++) {
int n1 = v[i].second.first;
int n2 = v[i].second.second;
int score = v[i].first;
if (find(n1) != find(n2)) {
ans += score;
merge(n1, n2);
res[n1].push_back(n2);
res[n2].push_back(n1);
}
}
cout << ans << "\n";
trace(0, -1);
}DFS, MST를 이러한 관점으로 접근시켜 문제를 출제하신 출제자분이 정말 대단하다고 느껴진 문제.
정말 재미있게 풀었다.
'PS > BOJ' 카테고리의 다른 글
| [BOJ] 백준 19700. 수업 (Gold I) (0) | 2021.09.29 |
|---|---|
| [BOJ] 백준 22355. 말뚝 (Platinum II) (0) | 2021.09.29 |
| [BOJ] 백준 4013. ATM (Platinum II) (0) | 2021.09.21 |
| [BOJ] 백준 21606. 아침 산책 (Gold III) (0) | 2021.09.18 |
| [BOJ] 백준 22876. 츠바메가에시 (Platinum IV) (0) | 2021.08.26 |